|
|
|
در این وبلاگ سعی خواهم کرد پروژه های درسی خود را با هم کلاسی هایم و دانشاموزان دیگر به اشتراک بگذارم.
طبقه بندی موضوعی
-
خانه
(۲) -
انرژی های نو
(۵) -
Soccer
(۲) -
ریاضی
(۲) -
دریا ها و اقیانوس ها
(۳) -
ایران
(۴) -
Technology
(۲) -
Food
(۴) -
کارتون
(۵) -
هنر
(۶) -
Famous Names
(۲)
خلاصه آمار
کلمات کلیدی
Zhang Ziyi
Tom Cruise
کاخ
فنگ شویی
آشپزخانه
teves
Carlos Teves
مثلث
دریای خَزَر
انرژی خورشیدی
انرژی باد
انواع انرژی ها
لباس محلی اقوام ایرانی
ریاضیات
رایانه
computer
هنر
نقاشی
آبرنگ
زیباییشناسی
تفاوت قطب شمال و جنوب
جاذبه های دیدنی و زیبای ایران
جاذبه های دیدنی ایران
دریای مرمره
مصر باستان
دایناسور
انرژی موج
پیتزای نیویورکی
انواع پاستا
ورزش شنا
بایگانی
- تیر ۱۳۹۵(۲)
- ارديبهشت ۱۳۹۴(۱۰)
- فروردين ۱۳۹۴(۲)
- اسفند ۱۳۹۳(۱۰)
- بهمن ۱۳۹۳(۱۴)
- دی ۱۳۹۳(۳)
آخرین مطلب
-
۹۵/۰۴/۲۰Zhang Ziyi
-
۹۵/۰۴/۲۰Tom Cruise
-
۹۴/۰۲/۱۸کتاب
-
۹۴/۰۲/۰۶Mr. Bean
-
۹۴/۰۲/۰۶والت دیزنی
-
۹۴/۰۲/۰۶Minions film
-
۹۴/۰۲/۰۶Tom and Jerry
-
۹۴/۰۲/۰۶باباسفنجی شلوارمکعبی
-
۹۴/۰۲/۰۲تاثیروخواص توت فرنگی برشادابی بدن
-
۹۴/۰۲/۰۲کاخ گلستان



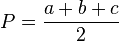 است. این فرمول به
است. این فرمول به 